清华oj pa3题解

就仅仅是记录一下（反正也不会有人看的

Description

As shown in the following figure, If another lighthouse is in gray area, they can beacon each other.

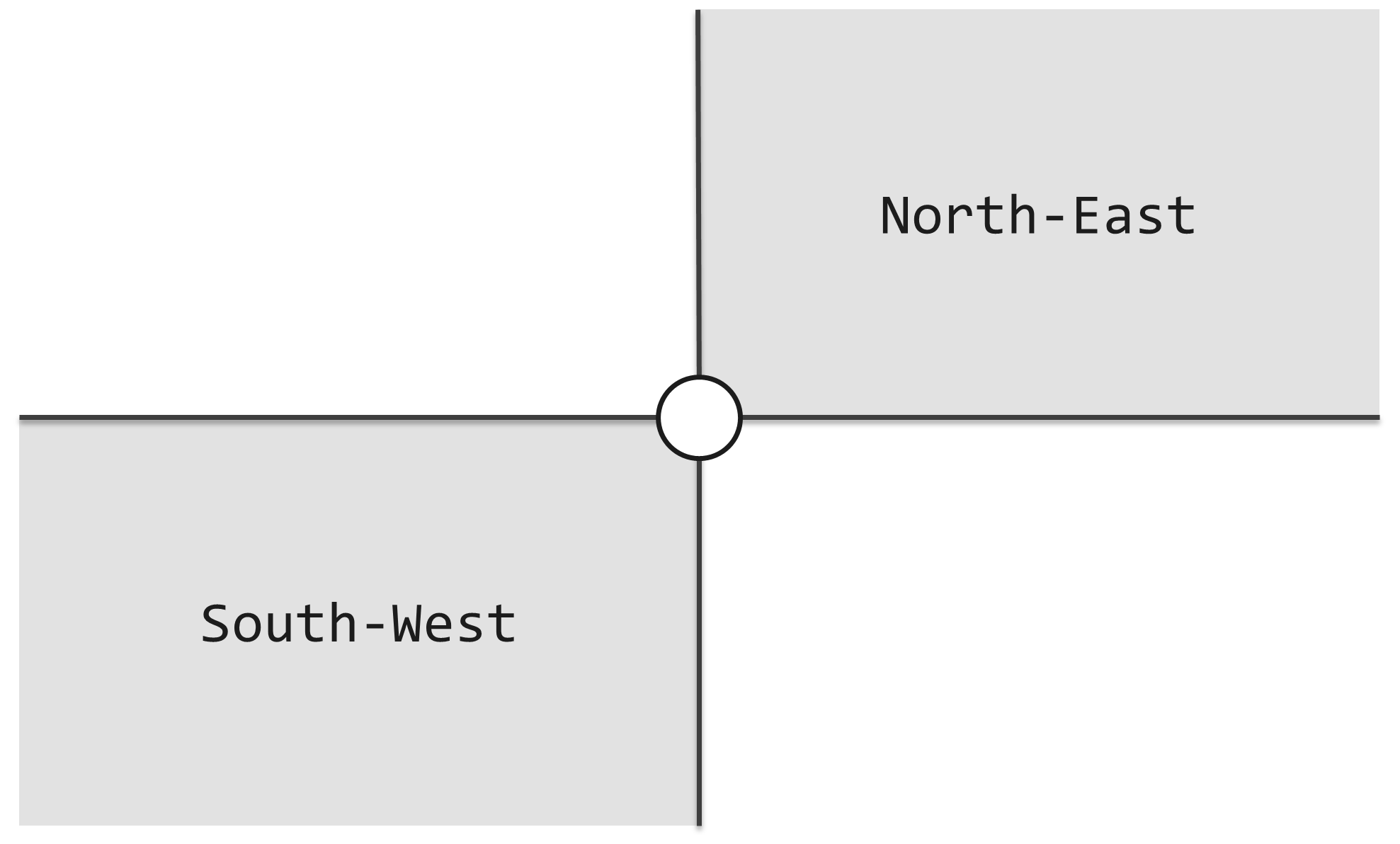
For example, in following figure, (B, R) is a pair of lighthouse which can beacon each other, while (B, G), (R, G) are NOT.

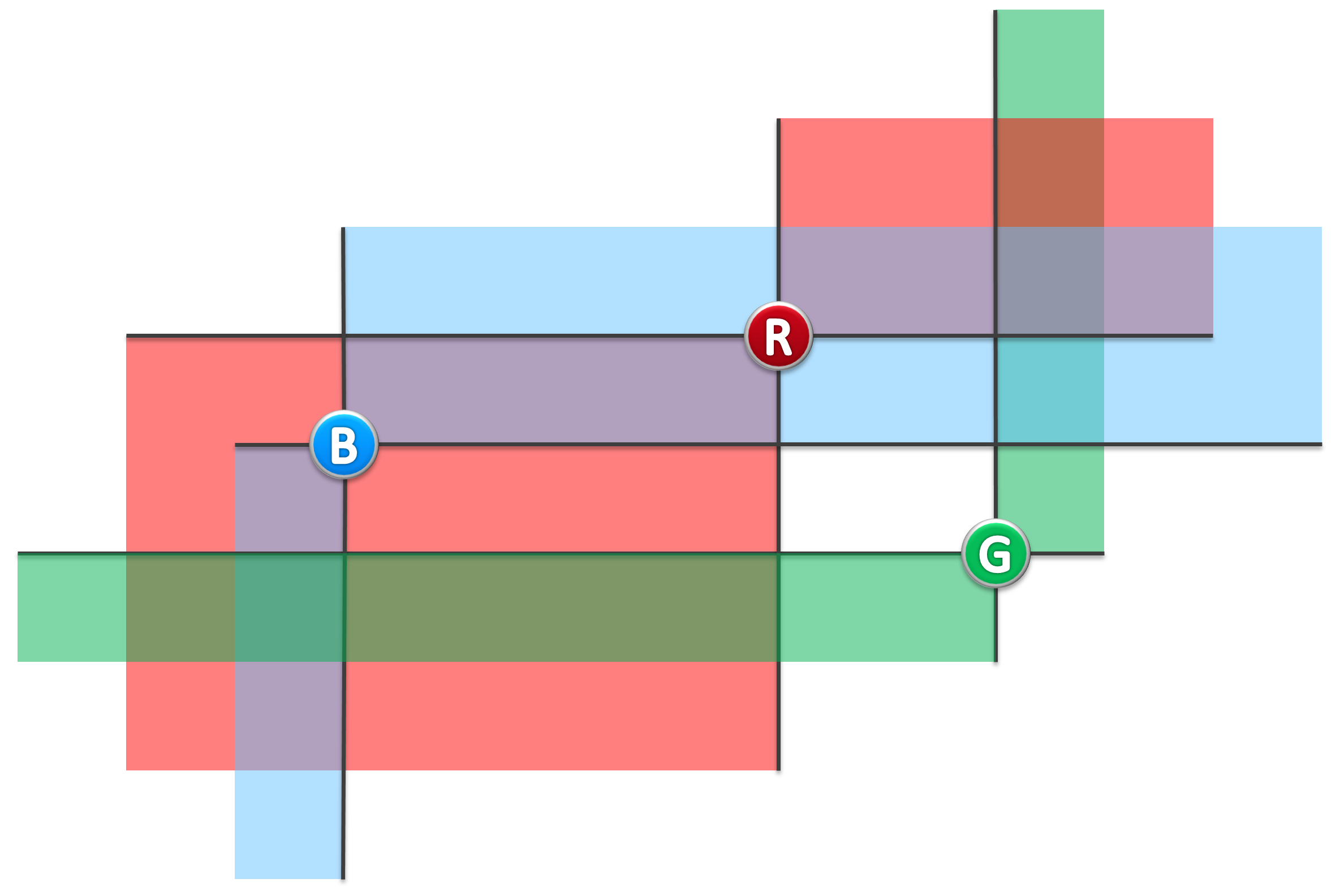
Input

1st line: N

2nd ~ (N + 1)th line: each line is X Y, means a lighthouse is on the point (X, Y).

Output

How many pairs of lighthourses can beacon each other

( For every lighthouses, X coordinates won't be the same , Y coordinates won't be the same )

Example

Input

3
2 2
4 3
5 1

Output

1

Restrictions

For 90% test cases: 1 <= n <= 3 * 10⁵

For 95% test cases: 1 <= n <= 10⁶

For all test cases: 1 <= n <= 4 * 10⁶

For every lighthouses, X coordinates won't be the same , Y coordinates won't be the same.

1 <= x, y <= 10^8

Time: 2 sec

Memory: 256 MB

Hints

The range of int is usually [-2³¹, 2³¹ - 1], it may be too small.

描述

海上有许多灯塔，为过路船只照明。

图一

如图一所示，每个灯塔都配有一盏探照灯，照亮其东北、西南两个对顶的直角区域。探照灯的功率之大，足以覆盖任何距离。灯塔本身是如此之小，可以假定它们不会彼此遮挡。

图二

若灯塔A、B均在对方的照亮范围内，则称它们能够照亮彼此。比如在图二的实例中，蓝、红灯塔可照亮彼此，蓝、绿灯塔则不是，红、绿灯塔也不是。

现在，对于任何一组给定的灯塔，请计算出其中有多少对灯塔能够照亮彼此。

输入

共n+1行。

第1行为1个整数n，表示灯塔的总数。

第2到n+1行每行包含2个整数x, y，分别表示各灯塔的横、纵坐标。

输出

1个整数，表示可照亮彼此的灯塔对的数量。

样例

见英文题面

限制

对于90%的测例：1 ≤ n ≤ 3×10⁵

对于95%的测例：1 ≤ n ≤ 10⁶

全部测例：1 ≤ n ≤ 4×10⁶

灯塔的坐标x, y是整数，且不同灯塔的x, y坐标均互异

1 ≤ x, y ≤ 10^8

时间：2 sec

内存：256 MB

提示

注意机器中整型变量的范围，C/C++中的int类型通常被编译成32位整数，其范围为[-2³¹, 2³¹ - 1]，不一定足够容纳本题的输出。

题解：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
//typedef long L;
long mergesort(long left, long right);
long merge(long left, long mid, long right);
int Cmp(const void* l1_, const void* l2_);
struct  Point
{
    long x, y;
};
Point p[4000005];
int main() {
    long num;
    scanf("%ld", &num);
    memset(p, 0, 4000005 * sizeof(Point));
    for (int i = 0; i < num; i++) {
        scanf("%ld%ld", &p[i].x, &p[i].y);
    }
    qsort(p, num, sizeof(Point), Cmp);
    cout << (long)num * (num - 1) / 2 - mergesort(0, num) << endl;
}


long mergesort(long left, long right) {
    if (right - left < 2) return 0;
    long mid = (right + left) >> 1;
    long temp[3];
    temp[0] = mergesort(left, mid);
    temp[1] = mergesort(mid, right);
    temp[2] = merge(left, mid, right);
    long res = temp[0] + temp[1] + temp[2];
    return res;
}

long merge(long left, long mid, long right) {
    Point* point1 = p + left;
    long temp1 = mid - left;
    Point *point2 = new Point[temp1];
    for (long i = 0; i < temp1; i++) {
        point2[i].x = point1[i].x;
        point2[i].y = point1[i].y;
    }
    int temp2 = right - mid;
    long count = 0;
    Point* point3 = p + mid;
    for (int i = 0, j = 0, k = 0; j < temp1;) {
        if (k < temp2 && point2[j].y >= point3[k].y) {
            count += (temp1 - j);
            point1[i].x = point3[k].x;
            point1[i++].y = point3[k++].y;
        }
        /*if (k >= temp2 || point2[j].y < point3[k].y) {
            point1[i].x = point2[j].x;
            point1[i++].y = point2[j++].y;
        }*/
        else {
            point1[i].x = point2[j].x;
            point1[i++].y = point2[j++].y;
        }
    }
    //delete[] point2;
    return count;
}

int Cmp(const void* l1_, const void* l2_) {
    Point* l1 = (Point *) l1_;
    Point* l2 = (Point*)l2_;
    return l1->x - l2->x;
}

如果有什么问题或者建议，可以和我发邮件联系或者留言：

我的个人邮箱为：

ntdgy2001@gmail.com/12011211@mail.sustech.edu.cn/hudatu@163.com（任选一个（（（

感谢阅读！

文章地址：https://ntdgy.top/ntdgy/121

短链接为：https://s.ntdgy.top/5